St Blogg's - Matematicas

miércoles, 6 de mayo de 2020

4.Orden de los números enteros.

Stiven Moran mayo 06, 2020 0

Para un adecuado orden de los números enteros solo se necesita conocer su ubicación en la recta numérica, ya que en numero que se encuentra hacia la derecha en la tabla numérica será siempre mayor que una que se encuentra en la parte izquierda. Con este concepto ya esta entendido su orden, ya que sabemos que los números enteros negativos se encuentran en la parte izquierda de la recta numérica y los positivos hacia la derecha de la recta numérica.

Debemos tener en cuenta los tres siguientes puntos para determinar que numero es mayor según la clase de números enteros que sean como negativos o positivos.

· Dados dos números enteros positivos, es mayor el que tiene mayor valor absoluto.

· Dados dos números enteros negativos, es mayor el que tiene menor valor absoluto.

· Un número positivo siempre es mayor que cualquier número negativo.

Con esta inducción estamos listos para empezar con la resolución de nuestros ejercicios.

2. Representa cada pareja de números enteros en la recta numérica. Luego, escribe > o <, según sea el caso.

3. Escribe el signo > o <, según corresponda.

Comunicación.

4. Completa la Tabla 2.

*Anterior*	*Numero*	*Siguiente*
*-211*	*-210*	*-209*
*244*	*245*	*246*
*-63*	*-62*	*-61*
*+298*	*+297*	*+298*
*-158*	*-157*	*-156*
*-303*	*-302*	*-301*

5. Ordena de menor a mayor los números de cada grupo.

a. 25, -32, 24, -1, 0, -12.

-32, -12, -1, 0, 24, 25.

b. 12, 7, -20, 16, -13.

-20, -13, 7, 12, 13.

c. -54, 678, -249, 14, -24, 0, 190.

-294, -54, -24, 0, 14, 190, 678.

d. 32, 56, 17, -8, -41.

-41, -8, 17, 32, 56.

6. Indica si cada afirmación es verdadera (V) o falsa (F).

a. 3 está entre 1 y -1. ( F ).

b. -1 está entre -3 y 0. ( V ).

c. -2 está entre 0 y 5. ( F ).

d. 2 está entre - 1 y 1. ( F ).

e. 3 está entre -5 y 5. ( V ).

7. Escribe un número que cumpla la condición que se enuncia en cada caso.

a. -6 < -5

b. -4 > -5 > -6

c. |-8| = 8

d. -21 < -20 < -19

e. -4 < 5 < 8

f. -2 < -1 < 0

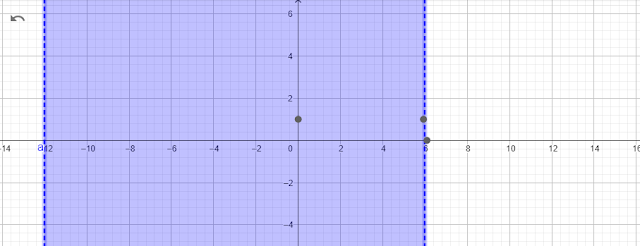
8. Representa en la recta numérica los números enteros que cumplan cada una de las condiciones dadas.

a. Son mayores que -12 y menores que +6.

b. Son menores que +24 y mayores que -1.

c. Son menores que +8 y mayores que -7.

d. Son menores que -7 y mayores que -24.

9. En la tabla 3 se presentan los puntos de ebullición aproximados de algunos elementos de la tabla periódica.

*Elemento Químico*	*Punto de Ebullición (°C)*
*Flúor*	*-188*
*Hidrógeno*	*-253*
*Argón*	*-186*
*Helio*	*-269*
*Nitrógeno*	*-196*
*Neón*	*-246*

a. ¿Cuál es el elemento químico con el mayor punto de ebullición? ¿Y con el menor?

* El Argón es el elemento con mayor punto de ebullición.

* El Helio es el elemento con el menor punto de ebullición.

b. Ordena, de menor a mayor, los elementos periódicos de la tabla según sus puntos de ebullición.

1. Helio

2. Hidrógeno.

3. Neón.

4. Nitrógeno.

5. Flúor

6. Argón

10. Tres fosas marinas tienen una profundidad de -5 534 m, -6 524 m y -4 321 m, respectivamente. ¿Cuál de las tres fosas marinas tiene mayor profundidad? ¿Cuál de las fosas es menos profunda?

· La que tiene -6524 es la que tiene más profundidad

· La que tiene -4321 es la que tiene menos profundidad.

Si deseas que te ayudemos con ejercicios de matemática de cualquier tema relacionado comenta y sigue nuestro Blogg.

Suscríbete a nuestros canales para empezar a publicar nuestros videos explicativos sobre el tema que deseas.

Referencia: Ministerio de Educación del Ecuador,2018.

viernes, 10 de abril de 2020

3.Valor absoluto de un número entero

Stiven Moran abril 10, 2020 0

El valor absoluto de un número es el numero que resulta presidiendo el signo.

Ejemplo 1: si tenemos el numero entero +50 su valor absoluto será 50 en este caso.

Ejemplo 2: en este caso usaremos -50 su valor absoluto también sera 50 el cual solo hemos precedido el signo negativo.

Concluyendo así que el valor absoluto de un numero sea positivo.

El valor absoluto se lo representa con este símbolo |a| .

Para empezar con la resolución debemos saber que un valor absoluto de cualquier número es positivo, pero, así como sabemos que es positivo en una variable no sabemos el origen verdadero de este ya que este será positivo, pero pudo haber sido positivo así que consideramos lo siguiente:

Resolución:

3. Determina estos valores absolutos.

a. |-3| = 3

b. |54| = 54

c. |0| = 0

d. |-(-11) | = 11

e. |-6| = 6

f. |-(-5) | = 5

g. |-a| = a

h. |-x| = x

i. |1+0| = 1

4. Calcula el resultado de cada operación.

a. |-3|*|8|

3*8 = 24

b. |-9|+|-13|

9+13 = 22

c. |-25| / |5|

25 / 5 = 5

d. |-30| / |-10|

30/10 =3

e. |-8|*|-4|

8*4 = 32

f. |-5|+|-10|

5+10 =5

g. |2|*|-9|

2*9 =18

h. |-24| / |6|

24 / 6 = 4

5. Indica si cada afirmación es verdadera (V) o falsa (F).

a. El valor absoluto de un número siempre es un entero positivo. ( V )

b. El valor absoluto de 0 es 1. ( F )

c. El valor absoluto de un número entero a positivo siempre es -a. ( F )

6. Halla el valor de x para que cada expresión sea verdadera.

a. |x| = 15.

1. x = +15

2. x = -15

b. |-3| = x

1. x = 3

c. |-x| =7

1. x = -5

2. x = +5

d. |x|=0

1. x = 0

e. |8| = x

1. x = 8

f. |-(-13) | = x

1. x = 13

g. |x-3| = 12

1. x-3 = -12

x = -9

2. x-3 = 12

x = 15.

7. Encuentra, en cada caso, el número entero que cumple la condición dada.

a. Su valor absoluto es 8 y está a la izquierda de 0.

Respuesta: - 8.

b. Su valor absoluto es 3 y está situado entre -4 y -2.

Respuesta: - 3.

c. Su valor absoluto es igual que el de su opuesto.

Respuesta: Todos los Reales

d. Su valor absoluto es 15 y es menor que 9.

Respuesta: -15

e. Su valor absoluto es 4 y se representa en la recta numérica a la derecha de -12.

Respuesta: -4

f. Su valor absoluto es 12.

Respuestas:

a. -12

b. +12

g. El valor absoluto de su opuesto es 7.

Respuestas:

a. -7

b. +7

8. Responde

¿Si a es un número entero, ¿cuál es el valor absoluto de -[-(-a)]?

Cualquiera que sea el numero este siempre será positivo, así que la respuesta será:

|-[-(-a)]|= a

Ejemplo:

|-[-(-5)]| = |-[5]|=|5|=5

Cualquier número que pertenezca a los reales cumplirá con la condición.

9. Señala con una X si la afirmación es verdadera o falsa.

10. Escribe el número que cumple simultáneamente estas condiciones

a. Su valor absoluto es mayor que 5 y menor que 9.

-5, +5, -6. +6, -7, +7, -8, +8

b. Está comprendido entre -10 y 7.

(-10,7)

c. Su valor absoluto es menor que 5 y mayor que 3.

+4, -4.

11. Explica cuál puede ser la ubicación de dos puntos A y B sobre la recta numérica, si:

|A-B| = 13

Respuesta: la ubicación en una recta numérica puede darse en cualquier lugar de la recta numérica ya que la variable no esta establecida y por ello se puede elegir cualquier numero de la recta numérica que cumpla con lo dicho, ejemplo:

|500-513| = 13

|10-(-3) | = 13

Y así sucesivamente así que la respuesta sería: Todos los reales

Ya que podemos irnos moviendo por la recta numérica y tener como resultado el valor absoluto de 13 infinitamente con cualquier valor de A y B.

Resolución de problemas:

12. Buscando una dirección, Alejandro camino inicialmente siete cuadras en una dirección. Luego, se desplazo tres cuadras en la dirección contraria. ¿Cuántas cuadras camino en total?

Son 7 cuadras que se desplaza inicialmente

Mas 3 cuadras de regreso se diría

En total camino 10 cuadras. Ya que nos pide cuantas cuadras camino en total y camino 10.

13. Valeria hizo la siguiente afirmación: “mi hermano recorre una distancia de -400m de la casa hacia el colegio”. ¿Consideras que la afirmación es correcta o incorrecta? Explica.

La información es incorrecta una distancia es considera como un valor absoluto por lo que el enunciado debería ser 400m de distancia.

14. Un vehículo sale del estacionamiento y se desplaza 40m al norte. Luego, se devuelve sobre la misma calle y se traslada 70m hacia el sur y, finalmente, se mueve 20m hacia el sur. ¿Cuantos metros recorrió en total el vehículo?

El vehículo en total recorrió una distancia de

40 + 70 + 20 = 130

Ya que no nos pregunta la distancia que separa del punto de partida al punto final.

15. Un pájaro elevándose en el aire, y un buzo sumergido en el mar, se encuentran a la misma distancia del nivel del mar. ¿A qué altura se encuentra el pájaro y a que profundidad se encuentra el buzo, si los separan 86m?

2x=86

X=43

El pájaro se encuentra a una altura de +43m

Y el buzo se encuentra a una profundidad de -43m

Si deseas que te ayudemos con ejercicios de matemática de cualquier tema relacionado comenta y sigue nuestro Blogg.

Suscríbete a nuestros canales para empezar a publicar nuestros videos explicativos sobre el tema que deseas.

Referencia: Ministerio de Educación del Ecuador,2018.

jueves, 27 de febrero de 2020

2. Números Enteros

Stiven Moran febrero 27, 2020 0

2.1 El conjunto de los Números Enteros.

Los matemáticos de la antigüedad no se bastaban con los numero naturales para poder entender la matemática de la manera correcta, así que empezaron a utilizar los números negativos para darse abasto de todos los conocimientos que nos querían dar a entender.

De esta manera se tiene el conjunto de los números enteros (Z), el cual está conformado por enteros positivos (+Z), y los enteros negativos (-Z).

Los números enteros negativos van precedidos por el signo menos (-).
Los números enteros positivos van precedidos por el signo más (+).

2.2 Opuesto de un número entero.

Cada número entero tiene su contraparte, así como en los videojuegos siempre existe un bueno y un malo. Tenemos que un número entero positivo cualquiera que sea este tendrá su contraparte negativo, o viceversa, ejemplo:

Resolución:

Desarrolla tus destrezas:

Comunicación.

Escribe un número entero que exprese la cantidad mencionada en cada caso.

a. La cima de la montaña está a 568 m de altura.

Respuesta: +568

b. Pitágoras nació en el siglo VI a. C.

Respuesta: -VI

c. El submarino está a 120 m de profundidad.

Respuesta: -120

d. La temperatura de la ciudad es de 5 ºC bajo cero.

Respuesta: -5

e. Pablo consignó $ 500 en su cuenta de ahorros.

Respuesta: +500

f. Sofía debe $350 al banco.

Respuesta: -350

3. Explica el significado de los números enteros utilizados en las siguientes expresiones.

a. La temperatura mínima registrada hoy fue de -3 ºC.

Respuesta: Nos da entender que la temperatura en una escala de grados Celsius fue de -3 ya que en esta el lugar de referencia es 0 grados Celsius.

b. El buzo se encuentra a -50 m.

Respuesta: Cuando un buzo se sumerge en agua se toma como punto de referencia el nivel del mar, así que el enunciado hace referencia que se encuentra a 50 metros de profundidad.

c. El alpinista está a +600 m.

Respuesta: El alpinista en este caso se encuentra a 600 metros de altura.

d. El ascensor quedó detenido en el piso -2.

Respuesta: El ascensor se quedo detenido 2 pisos debajo de la planta baja.

e. La Edad Media comenzó aproximadamente hacia el año +476.

Respuesta: En este caso se toma como referencia el sistema de fecha que utilizamos en la mayoría de los países el cual es el católico que comienza a ejecutarse después del nacimiento de Cristo. Así que tenemos que la edad media comenzó en el año 476 D.C

f. El estado de cuenta es de $ 700.

Respuesta: En este caso la respuesta seria la misma. Tenemos $700 en nuestra cuenta de banco.

5. Indica si cada afirmación es verdadera (V) o falsa (F).

a. El opuesto de un entero negativo es negativo. (F).

b. El opuesto del opuesto de un número positivo es negativo. (V).

c. La distancia entre dos números opuestos es el doble de la distancia entre uno de los números y el 0. (V)

d. El opuesto de un número entero positivo es negativo. (V).

6. Determina y escribe número entero que debe ir en cada casilla.

7. Ubica los números de cada grupo en la recta numérica.

8. Observa la Figura 13 y resuelve.

a. ¿A qué profundidad con respecto al nivel del mar se encuentra cada uno de los buzos?

El primer buzo se encuentra a -20 del nivel del mar.

El segundo buzo se encuentra a -40 del nivel del mar.

b. ¿A qué altura con respecto al nivel del mar se encuentra el avión?

El avión se encuentra a +40 del nivel del mar.

c. ¿A qué profundidad con respecto al nivel del mar se encuentra el pez amarillo?

El pez amarillo se encuentra a -50 del nivel del mar.

d. ¿En qué punto con respecto al nivel del mar se encuentra el barco?

El barco se encuentra en 0 del nivel del mar.

e. ¿Qué distancia separa el avión del pez más amarillo?

En este caso sumamos -50 que en su distancia es = 50 mas 40 que se encuentra el avión tenemos que 50+40=90

Respuesta = 90

Resolución de problemas

9. Analiza cada situación y responde las preguntas.

a. ¿Qué número se encuentra 4 unidades a la izquierda de 21? ¿Cuál es su opuesto?

Respuesta: 17 su opuesto es -17

b. El entero m está 5 unidades a la izquierda de n. Si n = -2, ¿cuál es el valor de m?

Respuesta = -7

c. Desde a hasta b hay 8 unidades. Si a = -3, ¿qué valores puede tener b?

Respuesta 1: Si fuera hacia la derecha b = 5

Respuesta 2: Si fuera hacia la izquierda b = -11

d. Los enteros m y n están separados por 10 unidades. Si la distancia de m a 0 es de 3 unidades, ¿cuáles son las posibles distancias de n a 0?

Respuesta 1: si m = 3, por la izquierda n a 0 distancia 7, por la derecha 13

Respuesta 2: si m = -3, por la izquierda n a 0 distancia 13, por la derecha 7

e. Un número positivo está al doble de unidades de 0 que un número negativo, y los dos están separados por 27 unidades. ¿Cuáles son esos números?

Respuesta: -9 y 18.

10. Para atrapar un pez, dos gaviotas se sumergen en el mar. La primera se sumerge a 45 cm y la otra, a 60 cm. Si el pez se encuentra a 50 cm de profundidad, ¿cuál de las dos gaviotas está más cerca de alcanzarlo?

El pez que se sumergió a 45 esta más cerca de atrapar ya que está a 5 unidades de distancia mientras que el de 60 se encuentra a 10 unidades de atraparlo.

Si deseas que te ayudemos con ejercicios de matemática de cualquier tema relacionado comenta y sigue nuestro Blogg.