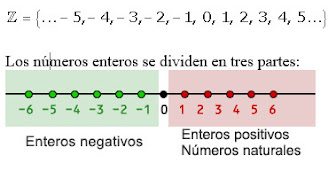
Conjunto de números enteros.

El conjunto de los números enteros está conformado por el conjunto de los números enteros positivos y el conjunto de los números enteros negativos, De esta manera se tiene el conjunto de los números enteros (Z), el cual está conformado por enteros positivos (+Z), y los enteros negativos (-Z).

El valor absoluto de un número es el numero que resulta presidiendo el signo.

Ejemplo 1: si tenemos el numero entero +50 su valor absoluto será 50 en este caso.

Ejemplo 2: en este caso usaremos -50 su valor absoluto también será 50 el cual solo hemos precedido el signo negativo.

Concluyendo así que el valor absoluto de un numero sea positivo.

El valor absoluto se lo representa con este símbolo |a|  .

Para empezar con la resolución debemos saber que un valor absoluto de cualquier número es positivo, pero, así como sabemos que es positivo en una variable no sabemos el origen verdadero de este ya que este será positivo, pero pudo haber sido positivo así que consideramos lo siguiente:

Evaluación formativa.

1. Completa la siguiente tabla con el número correspondiente.

Situación	Numero Entero
Estoy a 200 m bajo el nivel del mar.	+200
Luis depositó $ 450.	+450
Carlos retiró $ 35 dólares de la cuenta.	-35
El ascensor está en el subsuelo 3.	-3
El avión ascendió 2 000 m.	+20000

 2. Escribe el numero entero asociado a cada situación.

a) La temperatura ambiente es de 7 °C bajo cero.

    La temperatura es -7°C

 

b) Quito está a 2 800 m sobre el nivel del mar.

    Quito esta a +2800m del nivel del mar.

 

c) Pedro tiene ahorrado $ 300.

    Pedro tiene +300$.

 

d) Arquímedes nació en el año 287 a. C.

Arquímedes nació en el año -287.

 

e) Ana está en el quinto piso del edificio.

    Ana está en el piso +5.

 

f) La buceadora se encuentra a 45 m de profundidad.

   La buceadora se encuentra a -45 del agua.

3. Identifica los elementos y escribe en el conjunto correspondiente.

–23, 34, –67, 12, 17, –100, 56, 89, –80, 75, –9, –12

Z+ = {34,12,17,56,89,75}

Z- = {23, 67, 100, 80, 9, 12}

A=  -5                                       B =  -1                                 C =  +3

D =  +7                                     E = -3                                   F = +1

G =  +5                                    H = -8

6. Escribe (V) verdadero o (F) falso según corresponda.

a) Cualquier número positivo es mayor que un número negativo. ( V )

b) Entre dos números positivos es menor el que tiene mayor valor absoluto. ( F )

c) El cero es mayor que cualquier número positivo. ( F  )

d) El cero es mayor que cualquier número negativo. ( V  )

7. Ubica en la recta numérica las letras de los números solicitados.

A = 5                                      B = 2                             C = –3

D = –1                                    E = 6                             F = –6

9. Escribe cuatro números enteros que estén entre:

a) –5 y 9 ___-3,-1,1,3____

b) –15 y –3 ____-13,-10,-9,-7_______

c) –10 y 0 _____-9,-7,-5,-3________

10. Observa la recta numérica y responde.

a) ¿Cuántos números enteros se encuentran entre el 4 y –4?

Son 7 números enteros

b) ¿Cuántos números enteros se encuentran entre el 0 y –7?

Son 6 números enteros

c) ¿Cuántos números enteros se encuentran entre el 0 y –1?

Ninguno

11. Compara los pares de números y escribe los signos < o > según corresponda.

a) +8   >   –8                                             g) –5   <   –2

b) +8   >   –9                                            h) +6   <   +8

c) –2   <   +8                                            i) –5   <   +3

d) 0   <   +7                                              j) +9   >   –2

e) –5   <   –1                                            k) +30   >   –21

f) –17   >   –59                                        l) –23   <   +70

 

 12. Ordena en forma ascendente los números.

a) 4, –6, 9, 0, –8, 23, –50, 12, –12

   -50,-12,-8,-6,0,4,9,12,23

b) 17, –34, –15, 9, 5, 23, 12, –5, 20

  -34,-15,-5,5,9,12,17,20

c) 37, –4, –45, –9, –5, 3, –2, –15, 0

  -45,-15,-9,-5,-4,-2,0,3,37

13. Trabajen en equipo y resuelvan.

Escriban en tarjetas 10 números positivos y 10 negativos. Cada participante escoge al azar cuatro números y los ubica en una recta numérica.

14. Escribe el número que se encuentra antes y después de cada número dado.

Antes	Número	Después
-6	-7	-8
-7	-8	-9
11	12	13
-1	0	1

15. Halla el valor absoluto de cada número.

|–5| = 5                                            |+7| = 7                                        |–20| = 20

–|–2| = -2                                        |–|–3|| = 3                               –|–|–15|| = -15 

16. Escribe los números enteros que tengan por valor absoluto cada uno de los siguientes números:

a) 9                                      -9                                           +9       

b) 15                                   -15                                          +15         

c) 10                                   -10                                           +10    

d) 235                                -235                                         +235  

17. Escribe los cuatro siguientes términos de cada sucesión.

a) –10, –5, 0, 5, 10, 15,      20, 25, 30, 34

b) –20, –17, –14, –11, –8, –5,       -2, 1, 4, 7

c) 25, 20, 15, 10, 5, 0,        -5,-10,-15,-20

d) 6, –1, –8, –15, –22, –29,         -36, -43, -50, -57

 7.1 Igualdades.

¿Qué es una igualdad?

Una igualdad es la relación que existe entre dos expresiones matemáticas que representan el mismo valor. Estas vienen dadas por dos miembros los cuales están separados por el signo (=).

Ejemplo:

10 * 100 = 1000

40 + 50 = 45 + 45

Los conceptos son básicos por lo que si desean mas contenido de este tema ayúdanos suscribiéndote a nuestros canales para saber que te interesa, y nos ayudarías a continuar con nuestro proyecto.

7.2 Propiedades de las igualdades.

Para poder establecer las propiedades de las igualdades vamos a remplazar los números naturales con letras las cuales representaran nuestros números naturales.

Si a, b y c son cualquier número natural, tal que a = b, se puede establecer las siguientes igualdades:

-  a + c = b + c para todo a, b y c      y     a - c = b – c       para a > c y b > c.

- a x c = b x c    y     a / c = b / c para c diferente de 0 (a y b múltiplos de c).

Se establece que al adicionar o sustraer el mismo numero en ambas partes de la igualdad este va a tener el mismo valor

En la segunda propiedad se establece que si multiplicamos o dividimos para un determinado numero que sea diferente de cero obtendremos siempre el mismo número de la igualdad

7.3 Ecuaciones.

Una ecuación es una igualdad en la cual tenemos valores conocidos y valores desconocidos. El valor desconocido lo llamaremos incógnita estos valores generalmente por letras minúsculas del abecedario.

Una ecuación se resuelve cuando se encuentra el valor de la incógnita.

7.4 Ecuaciones aditivas y multiplicativas.

Tenemos dos tipos de ecuaciones los cuales son aditivas y multiplicativas.

- Las ecuaciones aditivas tienen las siguientes formas:

a + x = b                             x - a = b                           a – x = b

- Las ecuaciones multiplicativas pueden tener las siguientes formas:

a x x = b                           x / a = b                          a / x = b  

Teniendo en cuenta que a y b puede ser cualquier número natural.

7.5 Inecuaciones.

Una desigualdad es una expresión que compara dos cantidades las cuales no son igualdades. Pero al igual que las igualdades estas se las debe establecer un equilibrio, la desigualdad se la puede representar como una balanza inclinada hacia algunos de los lados.

Desarrolla tus destrezas

Ejercitación.

2. Determina si cada igualdad es correcta.

a. 45 + 27 = 31 + 36

72 = 71

Respuesta: La igualdad no es correcta

b. (3 x 12) = (72 / 2)

36 = 36

Respuesta: La igualdad es correcta

c. 4^3 = 8^2

64 = 64

Respuesta: La igualdad es correcta

d. (64 – 26 + 12) = 3^3

76 – 26 = 27

50 = 27

Respuesta: La igualdad no es correcta

e. (256 / 16) + 14 = 30 x 10

16 + 14 = 300

30 = 300

 Respuesta: La igualdad no es correcta

f. 34 + 28 – 19 – 20 + 18 = 32

80 – 39 = 32

41 = 32

Respuesta: La igualdad no es correcta

3. Resuelve cada ecuación y verifica su solución.

a. 23 + x = 52

-23 + 23 + x = 52 – 23

x = 29

b. 3 * n = 51

(3*n) / 3 = 51 / 3

n = 17

c. 8 + y – 12 = 1

y – 3 = 1

y – 3 + 3 = 1 + 3

y = 4

d. 5 * p = 30

(5 * p ) / 5 = 30 / 5

P = 6

 e. 50 = t – 1

50 + 1 = t – 1 + 1

51 = t

t = 51

f. 64 / 8 + u = 30

8 + u = 30

8 – 8 + u = 30 - 8

u = 22

g. r = 24 – 12 / 4

r = 24 – 3

r = 21

h. 56 / 8 - 7 = j

7 – 7 = j

0 = j

j = 0

i. 543 + 762 + h = 2653

1305 + h = 2653

1305 – 1305 + h = 2653 – 1305

h = 1348

j. 144 / s = 12

s * (144 / s) = 12 * s

144 = 12 * s

144 / 12 = (12 * s) / 12

 12 = s

s = 12 

4. Resuelve cada inecuación y dibuja su solución sobre una semirrecta numérica.

a. x > 7

b. y + 8 > 11

y + 8 – 8 > 11 – 8

y > 3  

c. n – 12 > 20

n – 12 + 12 > 20 + 12

n > 32

5. Escribe una ecuación que cumpla las condiciones dadas en cada caso.

a. Su solución es t = 14.

8 + t = 22

 

b. Su solución es y = 24.

y – 10 = 14

 

c. Es aditiva y su solución es 9.

12 + x = 21

 

d. Su solución es f = 14 y su lado izquierdo es 5 *f.

5f = 70

 

e. Su solución es h = 13 y el término de la derecha es h - 12.

1 = h -12 

Comunicación

 

6. Escribe dos inecuaciones cuya solución sea la que se representa en cada semirrecta numérica de la figura 5 a la figura 8.

1. X + 5 < 6

2. 15 > 14 + x

1. 5 + x < 15

2. x – 6 < 10 

Razonamiento

 

7. Califica como verdadera (V) o falsa (F) cada afirmación.

 

a. Todas las igualdades son ecuaciones.                                        (F)

b. Todas las inecuaciones son desigualdades.                              (V)

c. Todas las inecuaciones tienen infinitas soluciones.                  (V)

d. Todas las ecuaciones tienen solución.                                      (F)

e. Las ecuaciones equivalentes tienen la misma solución.         (V)

f. La solución de t + 10 = 10 es t = 1.                                           (F)

g. La solución de la ecuación h / 3 = 17 es h = 51.                     (V)

h. Las ecuaciones g + 4 = 5 y g - 2 = 1 tienen la                        (F)

misma solución.

 

8. Plantea una ecuación o una inecuación, según corresponda en cada caso, resuélvela y dibuja su solución sobre una semirrecta numérica

 

a. La diferencia entre un número y 8 es 10.

X – 8 = 10

 

b. El doble de un número es mayor que 18.

2x > 18

 

c. Un número sumado a 4 es igual a 11.

X + 4 = 11

 

d. El producto de 9 con cierto número es al menos 18.

9x = 18 

Razonamiento

 

9. Lee y soluciona.

Mauricio Andrés interpretó el enunciado “cinco veces un número más dos es igual a 17” mediante la ecuación 5 *(p+2) = 17. Por su parte, Adriana lo interpretó mediante la expresión 5*p+2 = 17.

a. ¿Cuál de ellos hizo la interpretación correcta?

Las dos interpretaciones son correctas.

 

b. ¿Cuál es la solución de la ecuación?

1. 1.4

2. 3

10. Resuelve.

¿En qué es diferente el gráfico de y+5 < 12 con respecto al gráfico de y+5 12?

La diferencia se ve reflejada en una grafica cuando pintamos el punto al que nuestra inecuación tiene como límite, depende si este pertenece a la inecuación o no pertenece. Si el punto esta pintado el numero esta incluido en la inecuación y si este no está pintado significa que este no pertenece.